2차원 평면에서 두 직선의 관계는 어떤 것들이 존재하는지와 교차점을 구하는 방법을 알아보도록 하겠습니다. 우선 2차원 평면이랑 축이 되는 Basis가 2개로 이루어진 공간을 의미합니다. 일반적으로 2차원이라고 하면 X축과 Y축을 이야기하기 때문에 이번 포스팅에서도 X축과 Y축을 기준으로 이야기를 하도록 하겠습니다. 다르게 이야기하면 XY 직교 좌표계가 되겠습니다.

두 직선 사이의 관계를 알아보기 전에 직선에 대해서 이야기를 하도록 하겠습니다. 직선은 무한한 길이를 갖는 선인데요. 두 점이 사이를 지나고 양쪽으로 무한하게 늘어나는 선을 직선이라고 합니다. 영어로는 Line 이라고 표현합니다. 이와 비슷한 개념이 있는데요. 바로 선분입니다. 선분은 두 점을 기준으로 사이에 유한한 선입니다. 영어로는 Segment 라고 합니다. 그리고 반직선이라는 개념도 있는데요. 이는 반은 직선이고 반은 선분인 선으로 한쪽으로 무한하게 늘어나는 선입니다.

따라서 선분을 만들기 위해서는 두 점이 필요합니다. 하지만 직선을 만들기 위해서는 두 점으로 만들 수도 있지만, 한 점과 방향벡터를 이용하여도 직선을 만들 수 있어요. 반직선도 두 점으로 만드는 방법 외에도 점과 방향벡터를 이용하는 방법도 있습니다.
이제 위에서 이야기한 2차원 직교좌표계에서 두 직선의 관계를 알아보도록 하겠습니다. 우선 결론부터 이야기하면 2차원 평면에서 두 직선의 관계는 딱 3가지로 나눌 수 있습니다. 앞으로 직선에 대한 이야기를 계속 하게 될 것 같으니까. 직선은 Line0, Line1, Line2, ... 으로 표현하고 직선 위의 임의의 점을 P0, P1, P2, ... 으로 표현하겠습니다. 그리고 직선의 방향벡터를 V0, V1, V2, .... 로 표현하겠습니다.
Line3는 P3를 지나고 V3의 방향벡터를 갖는 직선이라는 뜻이 됩니다.
1. 두 직선이 평행한 경우
2. 두 직선이 같은 경우
3. 두 직선이 한 점에서 만나는 경우
두 직선이 평행한 경우
한 직선을 Line0 이라고 하고 다른 직선을 Line1이라고 하겠습니다. Line0 과 Line1이 평행하기 위해서는 V0 와 V1 이 평행하여야 합니다. 벡터가 평행하다는 것은 V0 = α V1 이 성립하는 관계로 여기서 α 는 임의의 상수입니다. 그리고 P0와 P1은 다른 직선 위에 있지 않다면 두 직선은 평행한 경우에 성립합니다.
정리하면 Line0 = P0 + V0 * X과 Line1 = P1 + V1 * X이 평행하기 위해서는 V0 // V1 이고 Line0 ≠ P0 + V0 * P1 과 Line1 ≠ P1 + V1 * P0를 동시에 만족하여야 합니다.
두 직선이 같은 경우
이 경우는 Line0 과 Line1 에서 V0 과 V1은 서로 평행하다는 조건은 그대로 만족합니다. 하지만 여기서 P0과 P1이 서로 다른 직선 위에 있지 않아야된다는 조건을 만족하지 않는 경우, 즉 서로 다른 직선 위에 있어야 같은 경우가 됩니다. 즉 Line0 = P0 + V0 * P1과 Line1 = P1 + V1 * P0 이 만족하여야 하는 것입니다.
두 직선이 한 점에서 만나는 경우
위에서 알아본 2가지 경우를 제외한 경우라면 모두 한 점에서 만나는 경우입니다. 그렇다면 이제 두 직선이 한 점에서 만나는 경우 그 교점을 찾는 방법을 알아보도록 하겠습니다.
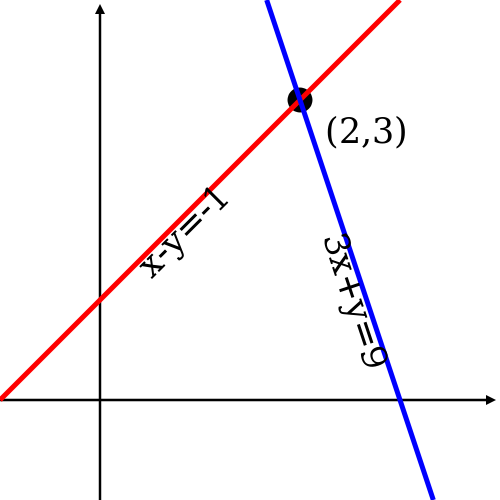
가장 쉬운 방법은 수학적으로 계산하는 방법이 있는데요. 이 방법은 아주 많은 포스팅에서 다루고 있기 때문에 기본적인 이야기만 하도록 하겠습니다. 2차원 직교좌표계에서 ax + by = c 로 직선을 표현할 수 있기 때문에 두 직선을 ax + by = c , dx + ey = f 로 표현할 수 있고 이를 미지수가 2개인 방정식으로 풀면 쉽게 답을 찾을 수 있습니다.
소스코드로 두 직선의 교점을 찾는 방법을 소개하도록 하겠습니다.

우선 이런 Point Class가 있다고 하겠습니다. 이때 교차점을 찾는 함수를

이런식으로 표현이 가능합니다. d 값이 0인 경우는 교차점이 존재하지 않는 조건이 됩니다. 따라서 위에서 평행하거나 같은지 확인하기 위해서 여러 코드를 작성할 필요없이 d 값만 구해서 0 인지 확인해주는 작업으로 교차점을 갖는지 확인이 가능한 것입니다.
'컴퓨터와 기하학' 카테고리의 다른 글
| LCS(Local Coordinate System) - GCS(Global Coordinate System) (0) | 2019.07.22 |
|---|---|
| 원(Circle)의 방정식과 3차원으로 확장 (0) | 2019.07.20 |
| 벡터의 외적(Cross Product)과 내적(Inner Product) (1) | 2019.07.17 |
| 평면(Plane) 에 대한 이야기 (0) | 2019.07.16 |
| [삼각망 만들기 / How to make Mesh] - # 02 (0) | 2019.02.21 |