기하학에서 평면은 매우 중요한 요소입니다. 점, 선, 면과 같이 각 차원에서 기본적인 요소가 되는 것들이죠. 이중에서 평면에 대해 이야기를 하도록 하겠습니다. 평면은 평평한 면으로 곡률이 없는 유클리드 평면입니다. 공간은 크게 유클리드 공간과 비유클리드 공간으로 나뉘는데요. 유클리드 공간은 곡률이 없는 공간입니다. 이는 수학자 유클리드가 연구하여 자신의 이름을 붙인 공간입니다. 이 공간에서는 5개의 공준이 성립하는 공간입니다. 여기서 5 공준이란
1. 서로 다른 두 점이 주어졌을 때, 그 두 점을 잇는 직선을 그을 수 있다.
2. 임의의 선분은 더 연장할 수 있다.
3. 서로 다른 두 점 A,B에 대해, 점 A를 중심으로 하고 선분 AB를 한 반지름으로 하는 원을 그릴 수 있다.
4. 모든 직각은 서로 같다.
5. 임의의 직선이 두 직선과 교차할 때, 교차되는 각의 내각의 합이 두 직각(180도)보다 작을 때, 두 직선을 계속 연장하면 두각의 합이 두 직각보다 작은 쪽에서 교차한다.
이 5 공준은 일반적으로 생각했을때 충분히 이해가 되는 공간입니다. 비유클리드 공간은 안으로 혹은 밖으로 휘어져있는 공간이기 때문에 일반적으로 상상하기 어렵습니다.
잠시 이야기가 산으로 갔지만, 지금부터 다룰 평면은 유클리드 공간에서 정의되는 평면이란 것을 기억해주세요. 우선 일반적인 3차원에서 평면의 방정식은 ax + bx + cz = d 로 정의할 수 있습니다. 여기서 (x, y, z)는 공간상에 점을 의미하는 것이고 a,b,c,d 는 해당 평면을 결정하는 숫자입니다. 여기서 x, y, z 는 미지수가 되기 때문에 점이 3개가 있다면 한 개의 평면을 정의할 수 있습니다.
평면을 구성하는 요소로 점과 방향벡터가 있는데요. 방향벡터는 평면에 수직한 벡터로 평면의 방향성을 알려주는 것입니다.

3차원 좌표계에서 xy 평면을 기준으로 방향벡터는 v (0, 0, 1)가 됩니다. yz 평면을 기준으로 방향벡터는 v (1, 0, 0)가 됩니다. 위에서 이야기한 3개의 점을 이용하여 평면의 구성요소를 생성할 수 있습니다. 각 점을 P0, P1, P2라고 하면 P0는 평면의 원점이 되고 P0에서 P1을 향하는 벡터와 P0에서 P2를 향하는 벡터를 외적하여 평면에서 수직한 방향벡터를 구하게 됩니다. 이 수직한 벡터를 V(a,b,c) 라고 하고 P0를 (p0, p1, p2)라고 하면 평면의 방정식은
a(x - p0) + b(y - p1) + c(z - p2) = 0
으로 만들 수 있습니다. 이때 두 벡터를 외적할때 어떤 점을 원점으로 선택하냐에 따라 2가지 평면이 나오게 되는데요. 법선벡터의 방향이 반대가 될 수 있습니다.
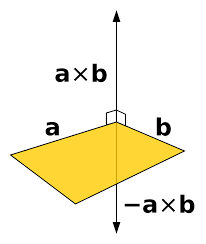
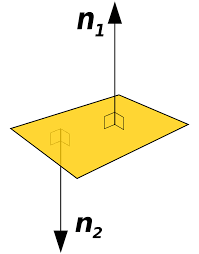
따라서 두 벡터를 외적을 할때 방향성을 원하는 방향으로 선택하여 평면을 생성해주셔야 합니다. 이는 컴퓨터 그래픽에서 면을 표현할때 두가지 면을 모두 표현하는 경우도 있지만, 한쪽 면만 표현하는 경우가 있기 때문에 중요한 것입니다. 이를 컴퓨터 그래픽에서는 Culling이라는 용어로 사용하는데요. 카메라의 시점을 기준으로 표현할 면을 선택하는 방법에 대한 원리를 기술하는 용어인데요.

왼쪽 해골의 경우 해골 안쪽면도 보이는 반면, 오른쪽 해골은 해골을 바깥면만 표현하게 됩니다. 만약에 속을 볼 수 없는 주사위와 같은 객체를 컴퓨터에서 표현하게 되면 안쪽면은 굳이 표현할 필요가 없기 때문에 메모리와 속도를 향상 시킬 수 있는 것입니다.
'컴퓨터와 기하학' 카테고리의 다른 글
| 원(Circle)의 방정식과 3차원으로 확장 (0) | 2019.07.20 |
|---|---|
| 평면에서 두 직선의 관계, 교차점 구하기 (0) | 2019.07.18 |
| 벡터의 외적(Cross Product)과 내적(Inner Product) (1) | 2019.07.17 |
| [삼각망 만들기 / How to make Mesh] - # 02 (0) | 2019.02.21 |
| [삼각망 만들기 / How to make Mesh] - # 01 (0) | 2019.02.21 |