컴퓨터를 통해서 기하학을 다루다보면 기초적인 수학개념이 많이 필요하고 이런 개념을 정확히 알고 있어야지 최적화된 알고리즘을 개발할 수 있습니다. 그래서 오늘은 행렬 연산에서 가장 기본적인 덧셈, 뺄셈, 곱셈, 스칼라에 대해서 이야기를 하겠습니다. 우선 행렬은 쉽게 연산을 할 수 있는 것이 아니고, 행렬을 연산하기 위해서는 조건이 필요합니다. 덧셈과 뺄셈을 하기 위해서는 행렬의 행과 열의 수가 일치해야하고, 곱셈을 하기 위해서는 곱하는 행렬의 앞 행렬과 뒤 행렬의 열과 행이 일치해야합니다. 그렇다면 이제부터 자세하게 다뤄보도록 하겠습니다.
1. 덧셈
두 행렬의 덧셈을 하기 위해서는 두 행렬의 열과 행이 서로 같아야합니다. 예를 들어서 2 x 3 행렬과 3 x 2 행렬은 각각 열과 행이 서로 다르기 때문에 덧셈이 불가능합니다. 2 x 3 행렬과 2 x 3 행렬은 덧셈이 가능합니다. 덧셈을 하는 방법은 각 행렬의 같은 위치의 원소들끼리 더하기를 해서 새로운 행렬에 같은 위치의 원소가 됩니다.
예를 들어보겠습니다. 아래 2 by 3 행렬 A와 2 by 3 행렬 B가 있다고 하겠습니다.


이때 행렬 A와 행렬 B를 더한 행렬을 C 라고 하면 다음과 같이 계산됩니다.
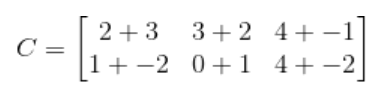
따라서 행렬 C는

가 되는 것을 알 수 있습니다.
2. 뺄셈
뺄셈도 덧셈과 마찬가지로 두 행렬의 크기가 같아야합니다. 그리고 덧셈을 뺄셈으로 바꾸면 되는 것입니다. 이에 대한 예제는 덧셈과 거의 비슷하기 때문에 따로 다루지 않겠습니다. 여기서 한가지 알아둬야하는 것이 있는데요. 행렬의 덧셈과 뺄셈은 교환법칙이 성립합니다. 즉 A + B = B + A 가 성립합니다. 그리고 A + B + C + ... + Z 를 순서를 아무리 바꿔서 연산을 하여도 결과는 그대로입니다.
3. 곱셈
행렬의 곱셈의 경우 행렬이 서로 붙는 부분이 있는데요. 이 붙는 부분의 크기가 같을때 곱셈을 할 수 있습니다. 예를 들어 2 by 3 행렬은 각각 아래와 같이 생겼는데요.

만약에 이렇게 생긴 두개의 행렬이 곱셈이 가능할까요? 정답은 불가능합니다. 왜냐면 곱셈은 앞의 행렬의 열과 뒤의 행렬의 행의 수가 같아야 곱셈이 가능합니다.

곱셈의 결과는 앞의 행렬의 행과 뒤 행열의 열만큼의 크기의 행렬이 됩니다. 위에 행렬이 2 by 3 행렬과 3 by 2 행렬의 곱은 2 by 2 행렬이 됩니다.
곱셈은 다음과 같이 이루어지는데요. 파란선을 기준으로 a, b, c와 A, C, E를 각각 곱해서 더하여 (1,1) 의 원소가 됩니다. 또 노란선을 기준으로 a, b, c와 B, D, F를 각각 곱해서 (1, 2)의 원소가 됩니다. 이런식으로 각 색깔별로 차례로 곱해서 행렬을 완성합니다. 실제 결과는 아래와 같습니다.

4. 스칼라
스칼라는 행렬의 크기와 상관 없이 행렬의 모든 원소에 일정한 상수를 곱하는 것입니다. 이는 각 행렬을 늘리는 것과 같은 의미인데요. 행렬을 n차원의 벡터로 생각한다면 모든 벡터를 늘리는 것과 같은 의미가 됩니다.

다음과 같은 행렬에 2를 스칼라배 한다면 각각의 원소에 2를 곱해서
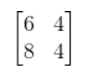
가 됩니다.
'컴퓨터와 기하학' 카테고리의 다른 글
| 행렬식 (Determinant) (0) | 2019.07.29 |
|---|---|
| 벡터란 무엇인가 - 벡터 연산 (0) | 2019.07.27 |
| 행렬의 기본 정리 - 행렬의 종류 (0) | 2019.07.25 |
| 3차원 이동행렬, 회전행렬(Translate Matrix, Rotation Matrix) (0) | 2019.07.24 |
| 행렬을 이용한 이동, 회전, 스케일 (Translate, Rotate, Scale) (0) | 2019.07.23 |