잡다한 이야기가 있...

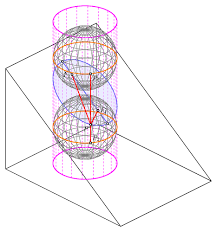
지난 2차원 직교좌표계에서 이동과 회전에 대해서 어떻게 움직이는지에 대해서 알아보았습니다. 관련 포스팅은 아래를 참고하시면 보실 수 있습니다. 그리고 오늘은 3차원 공간에서 이동행렬과 회전행렬에 대해서 알아보도록 하겠습니다. 여기서 말하는 공간은 유클리드 공간을 의미합니다.

https://math-development-geometry.tistory.com/50

우선 이동행렬에 대해서 이야기를 하고 회전행렬은 X축, Y축, Z축에 대한 회전을 알아보도록 하겠습니다. 그리고 나중에 시간이 된다면 임의의 축에 대한 회전도 알아보도록 하겠습니다. 

1. 이동행렬 (Translate Matrix)

이동행렬의 기본은 2차원 직교좌표계와 같이 점을 기준으로 움직인다고 생각하면 됩니다. 3차원 공간이기 때문에 점은 X축, Y축, Z축 이렇게 3가지 방향으로 움직일 수 있습니다. 이때 움직이는 방향의 값을 각각 Tx, Ty, Tz 라고 하면 점 (0, 0, 0)은 (Tx, Ty, Tz)로 이동하게 됩니다. 이를 행렬로 표현할 수 있습니다. 이때 사용하는 행렬은 4 by 4 행렬이고 이는 열과 행이 4개의 원소로 되어있습니다. 그리고 곱하는 점은 (x, y, z, 1) 인 벡터로 표현하게 됩니다. 

 행렬로 이렇게 표현할 수 있고 여기서 Tx, Ty, Tz는 각각 곱하는 점의 X, Y, Z와 더해지게 됩니다. 실제 이 행렬을 M이라고 하고, 이동하기 전의 점을 벡터로 표현한 것을 A라고 하고 결과를 B라고 하면 

B = MA 

가 성립하게 됩니다. 따라서 B는 (X + Tx, Y + Ty, Z + Tz, 1) , A는 (X, Y, Z, 1)이 됩니다. 

2. 회전행렬 (Rotation Matrix)

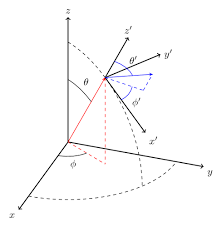
회전행렬은 일반적으로 X, Y, Z축에 대해서 회전을 하는 행렬을 이용해서 임의의 축을 기준으로 회전하는 행렬까지 확장하게 됩니다. 우선 이번 포스팅에서는 각 축에 대해서 회전하는 행렬에 대해서 알아보도록 하겠습니다. 회전행렬도 기존의 이동행렬과 마찬가지로 점을 기준으로 회전하는 것입니다. 점이 회전되면 모든 도형을 회전할 수 있습니다.

1) X축

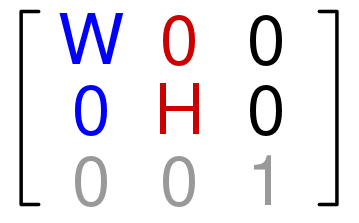
X축을 기준으로 회전하는 행렬은 아래와 같습니다.

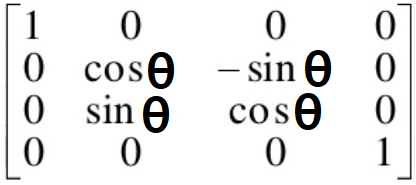
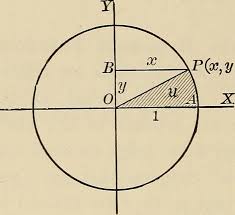
해당 행렬을 M이라고 하고 회전하기 전의 점을 B 회전 이후 점을 A라고 하면 A = MB 라고 표현할 수 있습니다. 이때 행렬을 곱하면 B 벡터의 X좌표는 1을 곱하기 때문에 변하지 않습니다. 그리고 나머지 Y축 Z축 좌표는 기존의 2차원 직교좌표계와 같은 방법으로 회전을 하는 것입니다. 

2) Y축

Y축을 기준으로 회전하는 행렬은 아래와 같습니다.

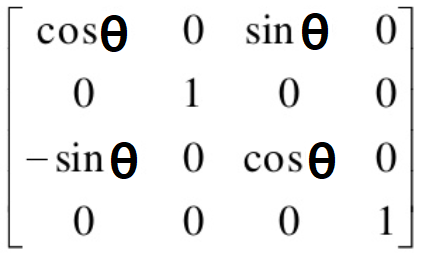
Y축을 기준으로 회전하는 행렬은 Y좌표에 1을 곱하기 때문에 변하지 않고 X축 Z축이 변하게 됩니다.

3) Z축

Z축을 기준으로 회전하는 행렬은 아래와 같습니다.

Z축을 기준으로 회전하는 행렬은 Z좌표에 1을 곱하기 때문에 변하지 않고 X축 Y축이 변하게 되는 것입니다. 이렇게 원리를 파악하게 되면 쉽게 행렬을 기억할 수 있습니다. 다음에는 이 3가지 행렬을 이용하여 임의의 축에 대해서 회전하는 방법에 대해서 이야기하도록 하겠습니다.

2차원 직교좌표계에서 모든 것은 점의 집합으로 표현할 수 있습니다. 예를 들면 선은 두개의 점을 잇는 점들의 집합이고 삼각형은 3개의 점을 잇는 선들을 만드는 점들의 집합이고, 원은 원의 중심을 기준으로 반지름만큼 떨어진 점들의 집합입니다. 이렇듯 2차원 직교좌표계에서 어떤 것을 표현하기 위해서 가장 기본이 되는 원소는 점입니다. 따라서 이 점을 회전하거나 이동하게 되면 모든 것을 회전하거나 이동할 수 있습니다. 이동, 회전, 스케일에 대해서 각각 어떻게 이루어져있고 어떤 방법으로 계산할 수 있는지 알아보도록 하겠습니다.

1. 이동 (Translate)

이동은 XY평면에서 2가지 방향이 존재합니다. X축과 평행한 방향, Y축과 평행한 방향 이렇게 두가지가 있고 이 두가지를 조합하면 모든 이동을 표현할 수 있습니다. 

점 A의 좌표는 (4, 3) 입니다. 맨 처음에 점 A가 (0,0) 에 있다고 가정할때 현재의 위치로 이동하기 위해서는 X축으로 4만큼 Y축으로 3만큼 이동하게 됩니다. 점 B의 좌표는 (-2, -3) 입니다. 맨 처음 점 B가 (0, 0)에 있다고 가정하면 이때 점 B는 X축으로 -2만큼 Y축으로 -3만큼 이동한 것입니다. 이것을 일반화하면

이동하기 전의 점을 A(x0, y0) 라고 가정할때 이 점이 A(x1, y1)로 이동했다면

X축으로 x1 - x0 만큼 y축으로 y1 - y0 만큼 이동하였다.

라고 말할 수 있습니다. 이는 방정식처럼 수학적으로 계산한 것인데요. 이를 행렬을 이용하여 표현할 수 있습니다. 2차원 직교좌표계에서 이동을 행렬로 표현하기 위해서 3 by 3 행렬이 필요한데요. 열과 행이 모두 3개씩인 행렬입니다. 

다음과 같은 이동 행렬을 이용하여 X축으로 X만큼 Y축으로 Y만큼 이동할 수 있습니다. 이 행렬을 M이라고 하면 점 A가 점 B로 이동할때 M 행렬을 이용한다고 하면 B = A * M 이 되는 것입니다. 

2. 회전 (Rotate)

회전은 2차원 직교좌표계이기 때문에 해당 평면 위에서만 회전을 한다고 생각해야 합니다. 즉 회전축은 가상의 Z 축이라고 생각하면 됩니다. 그리고 회전을 하는 기준점이 필요합니다. 그리고 얼마만큼 회전할지 각도가 필요합니다.  

점 A가 처음에 (5, 0) 에 있다가 원점(0, 0)을 기준으로 일정한 각도만큼 회전하여 A(4, 3)이 되었습니다. 이때 삼각함수를 이용하여 원점에서 점 A까지의 거리가 5인 것을 알고 삼각형의 밑변과 높이를 각각 점 A의 X좌표, Y좌표가 되면 회전이 되는 것입니다. 이를 원점을 기준으로 회전이 이루어졌지만, 항상 회전이 원점을 기준으로 이루어지지 않습니다. 이때는 해당 점을 기준으로 이동을 먼저 하여 원점으로 이동하여 회전을 하고 다시 이동을 할 수도 있고, 이동할 점이 원점에 있다고 가정하고 회전을 하고 다시 이동을 하는 방법이 있습니다. 이를 행렬로 표현하면

다음과 같이 표현할 수 있습니다. θ 는 회전 각도입니다. 해당 행렬에서 (1, 3)과 (2, 3)의 원소가 0인 것을 알 수 있는데요. 0인 이유는 원점을 기준으로 했다는 뜻이기 때문입니다. 만약에 원점을 기준으로 한 것이 아니라면 각각 회전 기준점의 X좌표, Y좌표가 들어가게 되는 것이죠.

3, 스케일 (Scale)

스케일은 늘리는 것을 의미하는데요. (1, 0)을 2배로 늘리면 (2, 0) 되는 것을 의미합니다. 스케일은 정말 간단한데요. X축으로 늘리고 싶은 스케일을 Sx라고 하고 Y축으로 늘리고 싶은 스케일을 Sy라고 하면 각 좌표에 Sx와 Sy를 곱하면 되는 것입니다. 따라서 이를 행렬로 표현하면

다음과 같은 행렬로 쓸 수 있습니다. 일반적으로 이동과 회전 행렬은 한번에 적용이 가능하지만 스케일은 조금 다르기 때문에 한번에 같이 적용하지는 않습니다. 

다음에는 2차원이 아닌 3차원에서 각 변환이 어떻게 이루어지는지 알아보도록 하겠습니다.

LCS(Local Coordinate System)과 GCS(Global Coordinate System)은 흔히 3차원 공간에서 물체를 표현하기 위해서 사용되는 방법입니다. 일반적으로 생각하는 3차원 공간좌표계에서 X, Y, Z축이 존재합니다. 

그림 1을 참고하면 LCS와 GCS를 쉽게 표현하였는데요. X, Y, Z축의 3차원 좌표공간이 GCS를 표현하고 안쪽에 X', Y', Z' 축의 3차원 좌표공간이 LCS를 표현합니다. 그렇다면 LCS와 GCS가 어떻게 사용되는지 알아보도록 하겠습니다. 3차원 공간에 원기둥이 있다고 가정해보겠습니다. 

이 원기둥은 높이가 h이고 반지름이 r이고 원기둥의 중심이 원점입니다. 이때 이 원기둥을 x축으로 회전시킨다고 생각을 하면 쉽게 상상을 할 수 있습니다. 그리고 x축으로 10만큼 y축으로 10만큼 이동한다고 생각을 할때도 쉽게 상상으로 어떤 결과를 만들어내는지 알 수 있습니다. 그런데 만약에 원기둥을 x축으로 10, y축으로 10 이동하고 x축을 기준으로 회전하고 z축으로 회전하는 동작을 계속 반복한다고 하면 어느 순간에는 이 원기둥이 어떻게 생겼고 어떻게 위치했는지 파악하기 어려운 순간이 오게 됩니다. 

이럴때 유용하게 사용될 수 있는 것이 바로 LCS와 GCS입니다. 볼링 게임을 예로 들어보겠습니다. 볼링 게임에는 볼링핀과 볼링공이 존재합니다. 그리고 경기장도 존재하겠습니다. 일단 경기장은 움직이지 않고 고정되어 있기 때문에 볼링장의 공간을 GCS로 고정합니다. 

X축 방향으로 볼링공이 굴러간다고 생각을 해보겠습니다. 이때 각 볼링핀에도 각각 좌표계가 생기게 되면 볼링공과 볼링핀의 위치나 회전을 쉽게 표현할 수 있게 됩니다. 이때의 좌표계를 LCS라고 부르게 되는 것입니다. 

이때 GCS를 기준으로 LCS를 계산하게 되면 실제 물체들의 움직이는 동작을 쉽게 계산할 수 있습니다. 볼링핀이 날아가는 괴적을 각 볼링핀의 LCS 원점으로 입력하면 볼링핀은 입력한 점을 기준으로 움직이고 볼링핀이 회전할때 x축으로 30도 y축으로 20도 z축으로 30도 회전하면서 날아간다는 계산이 나오면 각 볼링핀의 LCS의 축으로 회전을 하게 되면 모든 볼링핀들의 회전과 이동을 표현할 수 있게 됩니다. 실제로 게임을 만들거나 물체의 움직임을 표현하는 시뮬레이션에서는 각 물체들의 LCS를 계산하므로 움직임을 표현할 수 있습니다. 또 각 물체들의 움직임을 각각 병렬로 계산이 가능하기 때문에 빠르게 처리할 수 있습니다. 물론 여기서 각 물체끼리 충돌하는 것을 포함한다면 더 복잡한 기법들이 포함되지만 현재는 LCS와 GCS의 개념을 파악하기 위한 내용이기 때문에 충돌에 대한 이야기는 하지 않도록 하겠습니다. 

실제 각 LCS와 GCS는 수학적으로 회전이나 이동하는 행렬을 계산하는 방식으로 만들어지기 때문에 기본적인 수학적 내용을 알아둘 필요가 있습니다. 특히 회전행렬과 이동행렬과 같은 내용이 중요합니다. 

이와 관련된 내용은 다른 포스팅에서 다루도록 하겠습니다. 

현대 사회에서 경제에 영향을 미치는 요인은 정말 다양한 것들이 있습니다. 이런 다양한 변수들을 모두 통제할 수 없지만 각 변수에 대하여 많이 이해하고 있다면, 다른 사람보다 더 넓게 경제를 해석하고 예측할 수 있게 됩니다. 따라서 항상 정부의 정책을 유심히 지켜볼 필요가 있습니다. 하지만 정치 관련 기사나 소식을 듣다보면 자주 들었지만 항상 정확한 정의를 모르고 그냥 지나친 단어들이 있는데요. 여당과 야당, 좌파와 우파, 진보와 보수입니다. 이번 포스팅에서는 각 단어들의 정확한 뜻을 이해해보도록 하겠습니다.

1. 여당(與黨)과 야당(野黨)

여당의 "여"는 한자로 같이하다, 참여하다라는 뜻을 갖고 있습니다. 따라서 현재 대통령, 즉 정권을 잡고 있는 사람과 함께 하고 있는 집권당을 의미합니다. 과거 박근혜정부일때는 박근혜가 속한 자유한국당이 여당이 되었었고, 현재 문재인정부일때는 문재인이 속한 더불어민주당이 여당이 되는 것입니다. 

야당의 "야"는 변두리, 문밖이라는 뜻을 갖고 있습니다. 따라서 현재 대통령, 즉 정권을 잡고 있는 사람과 함께 하고 있는 집권당이 아닌 당을 의미합니다. 박근혜 정부에서는 야당은 자유한국당을 제외한 당을 의미하고 그러한 당들 중에서 가장 세력이 큰 당을 제1야당이라고 합니다. 더불어민주당이 제1야당이였죠. 현재는 자유한국당이 제1야당인거죠.

현재 국내 정당은 더불어민주당, 자유한국당, 바른미래당, 민주평화당, 정의당, 민종단, 대한애국당이 있습니다. (해당 정당은 원내정당을 기준으로 이야기합니다.)

2. 진보와 보수

진보와 보수를 나누는 기준은 정말 어려운 이야기인데요. 각 국가의 상황이나 사회제도에 따라서 다르게 되는데요. 현재 해당 국가의 상황이나 사회제도를 유지하고 이를 긍정적으로 생각하는 집단을 보수라고 보고, 이를 부정적으로 생각하면서 개선하기 위해서 노력을 한다면 진보라고 부를 수 있습니다. 하지만 한 정당이 모든 경제, 정치, 사회제도를 부정적으로만 혹은 긍정적으로만 생각하지 않고, 한 정당에서도 다양한 이야기가 나오기 때문에 자유한국당을 진보다 보수다. 혹은 더불어민주당을 진보다 보수다. 라고 명확하게 정의를 내리는 것이 쉽지 않습니다. 서로 정치적으로 필요할때 진보 혹은 보수가 되고 서로 보수다 서로 진보다 라면서 싸우기도 하는 것이 그들도 명확하지 않기 때문이죠. 

진보와 보수는 전체를 나누기보다는 경제제도, 이민정책, 교육정책, 복지정책과 같이 세부적으로 나눠 진보와 보수를 나누는 것이 훨씬 더 바람직한 생각이지 않을까 싶습니다. 

3. 좌파와 우파

좌파와 우파는 좌, 우... 즉 왼쪽과 오른쪽을 뜻하는 단어입니다. 그리고 당이 아닌 파라는 단어를 사용합니다. 사실 좌파와 우파는 정말 추상적인 개념으로 그 정의를 명확하게 정의할 수 없는 개념입니다. 한 국가를 기준으로 해당 국가의 정치가 성장해가면서 생기는 개념이라고 보시면 됩니다. 우리나라를 기준으로 과거 일제강점기, 6.25 전쟁, 미국, 일본, 중국과 같은 다양한 역사적 사실을 기반으로 좌파와 우파라는 개념이 생기게 되었는데요. 

6.25 전쟁을 기준으로 이야기를 시작하도록 하겠습니다. 6.25 전쟁이 끝나고 한반도는 남과 북으로 나뉘었습니다. 북에는 김일성, 남에는 이승만이 권력을 잡고 민주주의과 공산주의로 나뉘어졌습니다. 이후 이승만 정부는 미국의 도움을 받아 한국을 발전시키고 현재까지도 미국의 도움을 많이 받는 나라가 되었습니다. 그러면서 자유경제주의를 받아 들이고 자유로운 시장을 선호하는 사람들이 생겼고, 그런 사람들이 현재의 좌파의 주축을 이루고 있습니다. 따라서 자유로운 시장원리를 중요시 하고, 동등한 분배보다는 시장의 원리에 따라 분배를 원하는 사람들입니다. 

따라서 좌파는 공산주의와 같은 개념을 싫어하고, 정부입장에서는 경제에 최소한의 제한으로 시장이 스스로 움직일 수 있도록 합니다. 따라서 기업에 대한 규제를 적게 하고 최대한 자유를 보장하는 정책을 하게 됩니다. 그리고 선별적 복지를 통해 경제적으로 힘든 일부 계층에게 도움을 주게 됩니다. 즉 좌파는 국가의 발전을 위해서 최소한의 규제와 시장원리를 지지하는 행동을 합니다. 

우파는 좌파와 반대 위치에 있는 사람들입니다. 정부의 규제를 통해서 시장을 통제하는 것을 중요하게 생각합니다. 그리고 평등한 사회를 중요하게 생각합니다. 따라서 빈곤계층을 위한 정책을 많이 실행하고 북한에 쌀이나 소를 보내는 행동을 하면서 북한을 적으로 생각하지 않고 친해질 상대로 생각합니다. 또 통일과 관련된 정책을 많이 실행하였습니다.

전체적으로 정리를 하면 현재 시점에서 좌파는 자유한국당, 우파는 더불어민주당이 되겠습니다. 사실 좌파와 우파의 개념은 언제든지 바뀔 수 있지만 역사적인 관점을 기준으로 현재까지 만들어진 개념이기 때문에 하루 아침에 동전 뒤짚듯이 바꿀수 있는 개념은 아닙니다.  

일반적으로 2차원 직교좌표계(XY 평면을 기준으로한 좌표계)를 기준으로 원의 방정식은 (X - a) ^ 2 + (Y - b) ^ 2 = R ^2 이라고 표현할 수 있습니다. 여기서 X, Y는 미지수가 되는 것이고, a는 원의 중심의 X 좌표, b는 원의 중심의 Y좌표가 됩니다. 그리고 R는 원의 반지름입니다.

일반적으로 원을 2차원 직교좌표계에서는 쉽게 방정식으로 표현할 수 있습니다. 하지만 2차원 직교좌표계가 아닌 3차원 직교좌표공간에서는 어떻게 표현을 할 수 있을까요? 우선 원의 정의를 생각해보면 원의 중심이 되는 한 점을 기준으로 일정한 거리 (반지름) 만큼 떨어진 점들의 집합으로 표현할 수 있습니다. 이 정의를 3차원 직교좌표공간에서도 같게 유지하면서 점들을 찾으면 원을 생성할 수 있습니다.

여기서 구의 방정식과 원의 방정식은 다르다는 것을 인지하여야 합니다. 구은 영어로 Sphere라고 하며 공과 같은 모양을 한 도형을 의미합니다. 

구의 방정식은 (X - a) ^ 2 + (Y - b) ^ 2 + (Z - c) ^ 2 = R^2 으로 표현할 수 있고, X, Y, Z는 3차원 공간에서 임의의 점을 의미하고 (a, b, c)는 구의 중심, R은 구의 반지름을 의미합니다. 따라서 구의 중심에서 반지름 R만큼 떨어진 점들을 찾아서 Mesh로 표현하면 구가 되는 것이죠. 원과는 전혀 다른 이야기입니다. 

원을 정의하기 위해서는 평면을 먼저 알아야 합니다. 평면은 법선벡터를 갖은 무한히 평평한 면입니다. 이때 법선벡터는 해당 평면에 수직방향인 벡터를 의미합니다.

평면이 XY평면이라고 하면 법선벡터는 Z축에 평행한 벡터가 되는 것입니다. 이제 평면을 정의했다면 이제 원을 정의할 수 있게 됩니다. 원은 한 평면에서만 존재할 수 있기 때문입니다. 처음 원을 정의할때 한 평면에서 원의 중심과 반지름을 이용한다는 의미가 내포되어 있는 것이죠. 일반적으로 원이라고하면 평면에 정의된다는 것을 익숙하게 생각하기 때문에 대부분 표현을 생략하는 것입니다. 

만약에 ZX 평면에 (0,0,0)을 중심으로 하고 반지름을 5로 하는 원을 생성하고 싶다면 (X - 0) ^ 2 + (Z - 0) ^ 2 = R ^ 2 으로 표현되는 것이죠. XY평면이나 ZX평면과 같이 한 축에 수직인 경우 방정식으로 표현하기가 쉽겠지만, 임의의 평면에 대해서 원의 방정식을 구하는 것은 쉽지 않습니다. 따라서 평면, 원의 중심, 원의 반지름이라는 3가지 요소를 가지고 XY 평면으로 변환하여 방정식을 표현하게 됩니다.

예를 들면 3차원에서 두 원의 교점을 구하는 문제를 풀기 위해서, 우선 두 원의 평면이 같은 법선벡터를 갖는지, 확인을 한 뒤 두 원을 XY평면으로 이동하여 일반적인 두 원의 교점을 구하는 문제로 변환하여 해결하게 됩니다. 컴퓨터 기하학을 하기 위해서 이런 변환을 LCS to GCS 혹은 GCS to LCS 에 대한 이야기를 알아야합니다. 즉 3차원 공간에서 임의의 좌표계가 있을때, 이 좌표계를 원하는 공간의 좌표계로 변환하는 방법을 의미합니다. 다음에 시간이 되면 해당 내용도 다루도록 하겠습니다.

2차원 평면에서 두 직선의 관계는 어떤 것들이 존재하는지와 교차점을 구하는 방법을 알아보도록 하겠습니다. 우선 2차원 평면이랑 축이 되는 Basis가 2개로 이루어진 공간을 의미합니다. 일반적으로 2차원이라고 하면 X축과 Y축을 이야기하기 때문에 이번 포스팅에서도 X축과 Y축을 기준으로 이야기를 하도록 하겠습니다. 다르게 이야기하면 XY 직교 좌표계가 되겠습니다.

두 직선 사이의 관계를 알아보기 전에 직선에 대해서 이야기를 하도록 하겠습니다. 직선은 무한한 길이를 갖는 선인데요.  두 점이 사이를 지나고 양쪽으로 무한하게 늘어나는 선을 직선이라고 합니다. 영어로는 Line 이라고 표현합니다. 이와 비슷한 개념이 있는데요. 바로 선분입니다.  선분은 두 점을 기준으로 사이에 유한한 선입니다. 영어로는 Segment 라고 합니다. 그리고 반직선이라는 개념도 있는데요. 이는 반은 직선이고 반은 선분인 선으로 한쪽으로 무한하게 늘어나는 선입니다. 

따라서 선분을 만들기 위해서는 두 점이 필요합니다. 하지만 직선을 만들기 위해서는 두 점으로 만들 수도 있지만, 한 점과 방향벡터를 이용하여도 직선을 만들 수 있어요. 반직선도 두 점으로 만드는 방법 외에도 점과 방향벡터를 이용하는 방법도 있습니다.

이제 위에서 이야기한 2차원 직교좌표계에서 두 직선의 관계를 알아보도록 하겠습니다. 우선 결론부터 이야기하면 2차원 평면에서 두 직선의 관계는 딱 3가지로 나눌 수 있습니다. 앞으로 직선에 대한 이야기를 계속 하게 될 것 같으니까. 직선은 Line0, Line1, Line2, ... 으로 표현하고 직선 위의 임의의 점을 P0, P1, P2, ... 으로 표현하겠습니다. 그리고 직선의 방향벡터를 V0, V1, V2, .... 로 표현하겠습니다. 

Line3는 P3를 지나고 V3의 방향벡터를 갖는 직선이라는 뜻이 됩니다.

1. 두 직선이 평행한 경우

2. 두 직선이 같은 경우

3. 두 직선이 한 점에서 만나는 경우

두 직선이 평행한 경우

한 직선을 Line0 이라고 하고 다른 직선을 Line1이라고 하겠습니다. Line0 과 Line1이 평행하기 위해서는 V0 와 V1 이 평행하여야 합니다. 벡터가 평행하다는 것은 V0 = α V1 이 성립하는 관계로 여기서 α 는 임의의 상수입니다. 그리고 P0와 P1은 다른 직선 위에 있지 않다면 두 직선은 평행한 경우에 성립합니다. 

정리하면 Line0 = P0 + V0 * X과 Line1 = P1 + V1 * X이 평행하기 위해서는 V0 // V1 이고 Line0 ≠ P0 + V0 * P1 과 Line1 ≠ P1 + V1 * P0를 동시에 만족하여야 합니다. 

두 직선이 같은 경우

이 경우는 Line0 과 Line1 에서 V0 과 V1은 서로 평행하다는 조건은 그대로 만족합니다. 하지만 여기서 P0과 P1이 서로 다른 직선 위에 있지 않아야된다는 조건을 만족하지 않는 경우, 즉 서로 다른 직선 위에 있어야 같은 경우가 됩니다. 즉 Line0 = P0 + V0 * P1과 Line1 = P1 + V1 * P0 이 만족하여야 하는 것입니다. 

두 직선이 한 점에서 만나는 경우

위에서 알아본 2가지 경우를 제외한 경우라면 모두 한 점에서 만나는 경우입니다. 그렇다면 이제 두 직선이 한 점에서 만나는 경우 그 교점을 찾는 방법을 알아보도록 하겠습니다. 

가장 쉬운 방법은 수학적으로 계산하는 방법이 있는데요. 이 방법은 아주 많은 포스팅에서 다루고 있기 때문에 기본적인 이야기만 하도록 하겠습니다. 2차원 직교좌표계에서 ax + by = c 로 직선을 표현할 수 있기 때문에 두 직선을 ax + by = c , dx + ey = f 로 표현할 수 있고 이를 미지수가 2개인 방정식으로 풀면 쉽게 답을 찾을 수 있습니다. 

소스코드로 두 직선의 교점을 찾는 방법을 소개하도록 하겠습니다.

우선 이런 Point Class가 있다고 하겠습니다. 이때 교차점을 찾는 함수를 

이런식으로 표현이 가능합니다. d 값이 0인 경우는 교차점이 존재하지 않는 조건이 됩니다. 따라서 위에서 평행하거나 같은지 확인하기 위해서 여러 코드를 작성할 필요없이 d 값만 구해서 0 인지 확인해주는 작업으로 교차점을 갖는지 확인이 가능한 것입니다.